DEVOIR SURVEILLE N°9

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

télécharger le document au format open office

Exercice n°1 : 7 points

La courbe C_f ci-contre représente une fonction f définie et dérivable sur .

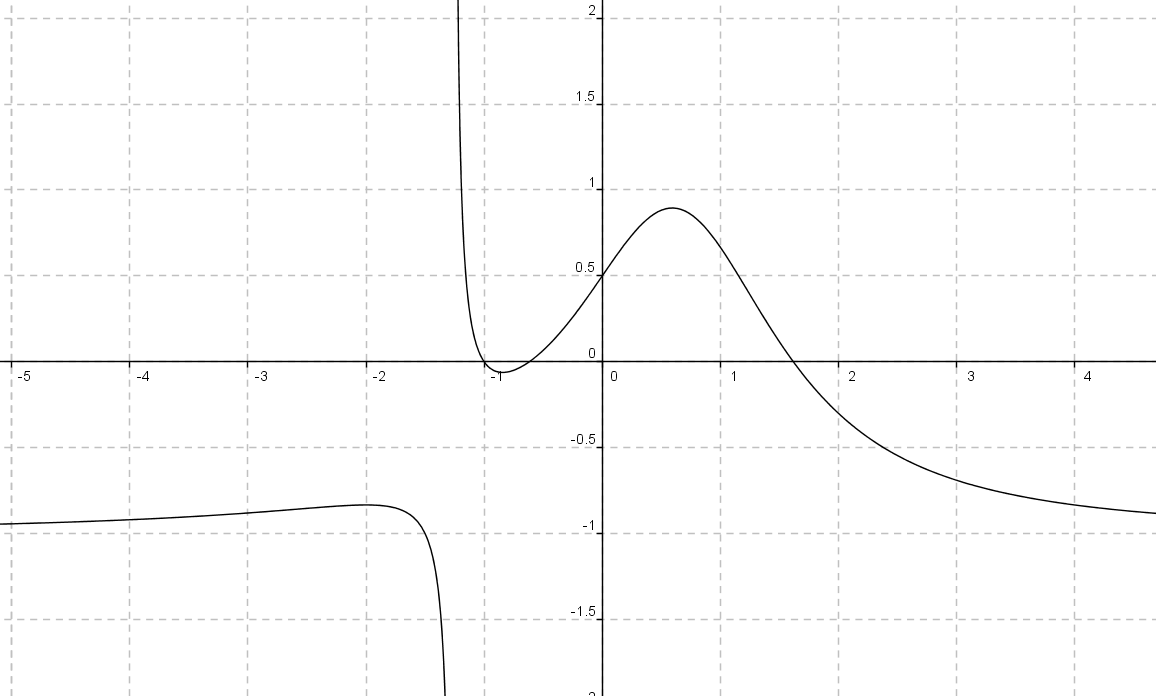
On note la fonction dérivée de la fonction f.

A partir du graphique :

1. Déterminer , et .

2. Déterminer , et .

3. Donner le signe de f '(x)

4. Donner le tableau de variations complet de f.

Exercice n°2 : 11 points

Soit f la fonction définie sur par ..

Sa courbe représentative dans un repère du plan, notée C_f , est donnée ci-dessous.

1. Démonter que pour tout , .

2. Donner, en justifiant, et . En déduire une asymptote à C_f.

3. Démontrer que la courbe C_f admet pour asymptote la droite d'équation .

4. On note la dérivée de la fonction f. Calculer et en déduire le tableau des variations de f.

5. Déterminer une équation de la tangente T à la courbe C_f au point d'abscisse 1.

Exercice n°3 : 2+1 points

Soit C la fonction définie pour tout x élément de l'intervalle par : .

La fonction C modélise le coût total de production, exprimé en milliers d'euros, de x milliers d'articles fabriqués.

Le prix de vente de chaque article produit est égal à 8,35 €.

1. On note la recette générée par la production et la vente de x milliers d'articles.

   Donner R(x) en fonction de x.

2. Le bénéfice est la fonction B définie sur l'intervalle par .

   1. Calculer

   2. étudier les variations de la fonction B.

   3. En déduire la production x₀ pour laquelle le bénéfice est maximal.

Quel est le montant en euro de ce bénéfice maximal.

 Bonnes vacances 