DEVOIR SURVEILLE N°4
DEVOIR SURVEILLE N°4
Durée 2h
Exercice n°1 : 3 points
Exprimer en fonction de x,
les dérivées des fonctions suivantes :
![]() et
et ![]() .
.
Exercice n°2 : 5 points
S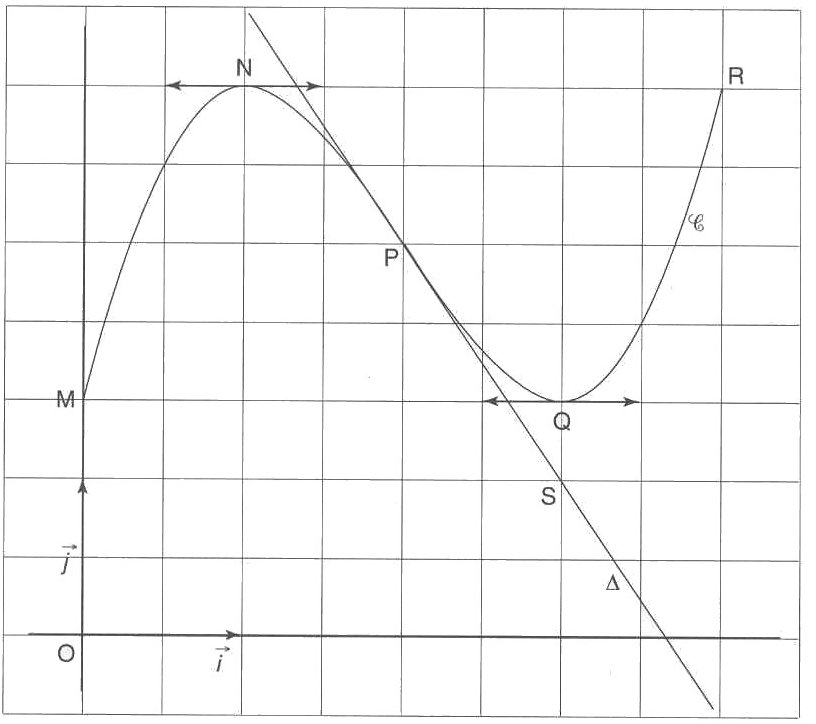 oit f la fonction définie
et dérivable sur l'intervalle [0; 4] dont la représentation graphique,
dans un repère orthonormal
oit f la fonction définie
et dérivable sur l'intervalle [0; 4] dont la représentation graphique,
dans un repère orthonormal ![]() est la courbe C
ci-dessous. Les points M, N, P, Q et R appartiennent à C.
est la courbe C
ci-dessous. Les points M, N, P, Q et R appartiennent à C.
Les coordonnées de M sont ![]() , celles de N sont
, celles de N sont ![]() , celles de P sont
, celles de P sont ![]() , celles de Q sont
, celles de Q sont ![]() et celles de R sont
et celles de R sont ![]() .
.
La courbe C admet en chacun des points N et Q une tangente parallèle à l'axe des abscisses.
La droite ![]() est la tangente à la courbe C
au point P; elle passe par le point S de coordonnées (3; 1).
est la tangente à la courbe C
au point P; elle passe par le point S de coordonnées (3; 1).
a) Déterminer graphiquement
![]() ,
,
![]() et
et ![]() .
.
b) Déterminer une équation de la droite
![]() .
.
La fonction f
est la dérivée d'une fonction F définie sur l'intervalle
[0 ; 4].
Donner le sens de variation de F.
Soit g
la fonction définie sur l'intervalle [0; 4] par
![]() .
.
Donner le tableau de variations de f et
en déduire le tableau de variations de n.
Exercice n°3 : 12 points
Soit la fonction h
définie sur ![]() par :
par : ![]() où m
et p
sont des nombres réels quelconques.
où m
et p
sont des nombres réels quelconques.
Justifier que h
est définie sur ![]() .
.
Calculer les nombres m
et p pour que ,
la courbe représentative de h,
passe par le point A de coordonnées
(2 ;0) et admette au
point B, d’abscisse
1, une tangente parallèle à la droite d’équation![]() .
.
On considère la fonction g
définie sur ![]() par :
par : ![]() .
.
a) Etudier les variations de g.
b) Donner le tableau de variations de g.(on
admettra que g se rapproche de 1 quand x
se rapproche de ![]() et quand x se rapproche de
et quand x se rapproche de
![]() ).
).
c) g admet-elle des extremums
sur ![]() ?
Sur
?
Sur ![]() ?
Et sur
?
Et sur ![]() ?
Justifier.
?
Justifier.
d) Prouver que
admet un centre de symétrie.
e) Donner une équation de la tangente à
au point d'abscisse 0.
f) Construire
dans un repère orthonormal bien choisi ainsi que les tangentes vues
précédemment.
g) Soit ![]() un nombre réel, démontrer que
un nombre réel, démontrer que ![]() est équivalent à
est équivalent à ![]() .
.
h) En déduire graphiquement, selon les valeurs de
![]() ,
le nombre de solutions de l’équation
,
le nombre de solutions de l’équation ![]() .
.
i) En déduire, sans calculer le discriminant, le nombre de racines
du polynôme :![]() .
.
Correction
Exercice n°1 : 3 points
p est de la forme :
![]() avec
avec ![]() et
et ![]() .
.
Donc ![]() .
.
Exercice n°2 : 5 points
a) ![]() ,
,
![]() et
et ![]() ce sont les coefficients directeurs des tangentes à la courbe.
ce sont les coefficients directeurs des tangentes à la courbe.
b) ![]() On a déjà le coefficient directeur on trouve l'ordonnée
à l'origine en utilisant que S appartient à
On a déjà le coefficient directeur on trouve l'ordonnée
à l'origine en utilisant que S appartient à
![]() et donc ses coordonnées vérifient l'équation de
et donc ses coordonnées vérifient l'équation de
![]() .
.
f est positive sur [0;4] donc F est croissante sur [0;4].
n est la composée de la fonction f suivie de la fonction inverse. La fonction inverse étant décroissante donc pour trouver les variations de n il suffit de faire les variations inverses de f.
Exercice n°3 : 12 points
pour que h
soit définie , il faut que le dénominateur ne soit pas égal
à zéro. On calcul le discriminant. Il est négatif
![]() donc
donc
![]() .
.
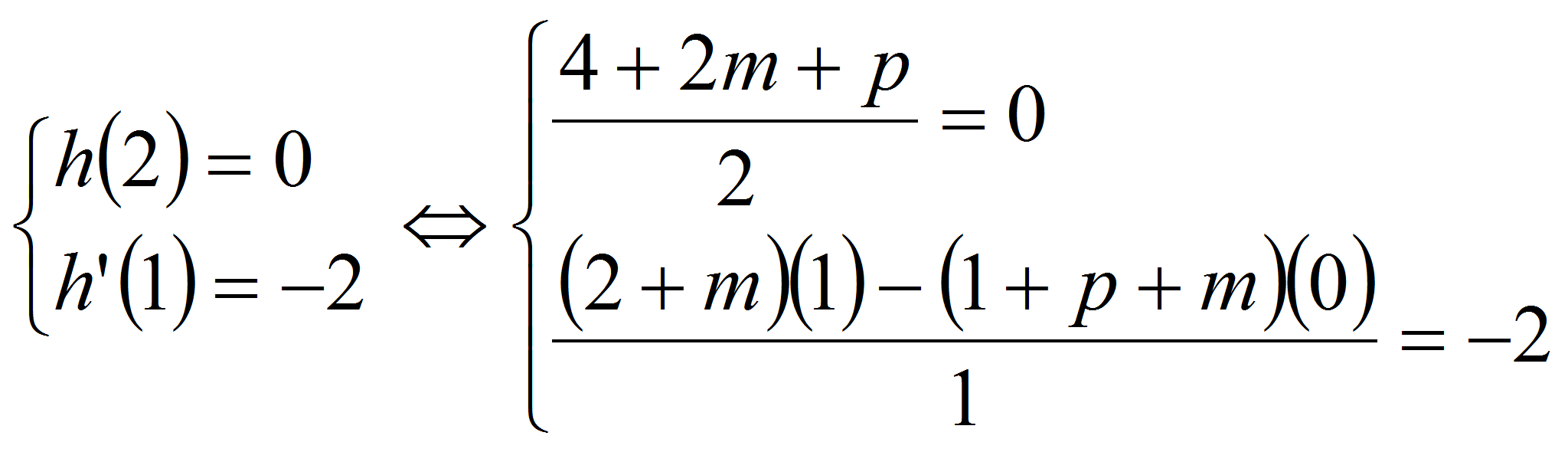 car
car ![]()
![]()
![]() Donc
Donc ![]()
a) On doit étudier le signe de
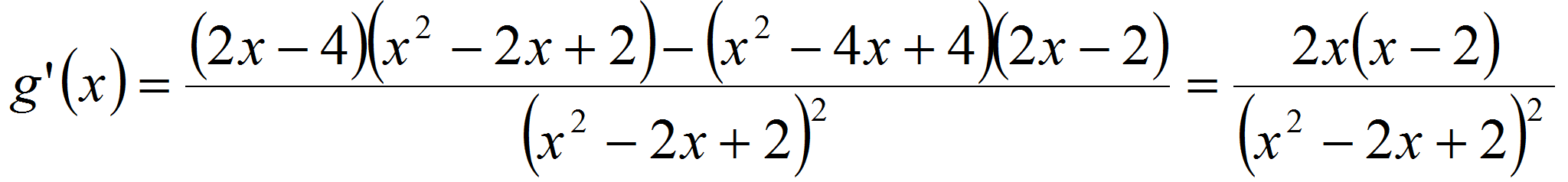
puis on étudie le signe de g'
en étudiant le signe de 4x
et celui de x-1:
![]() et
et ![]()
|
x |
- |
|||||
|
Signe de 4x |
- 0 + + |
|||||
|
Signe de x-1 |
- - 0 + |
|||||
|
Signe de g'(x) |
+ - + |
|||||
|
x |
- |
|
g |
1 0 |
c) g
admet un minimum 0 sur ![]() ,
mais pas de maximum. En effet ce maxi pourrait être 1, mais il n'existe
pas de réel r de
,
mais pas de maximum. En effet ce maxi pourrait être 1, mais il n'existe
pas de réel r de
![]() tel que g(r)=1.
tel que g(r)=1.
Par contre sur ![]() g(1)=1 donc 1 est le maximum.
g(1)=1 donc 1 est le maximum.
Sur ![]() ,
max 2 et min 0.
,
max 2 et min 0.
d) Le centre de symétrie est A(1;1). Pour le prouver, on prend un réel quelconque que l'on note h et on calcul g(1+h)+g(1-h) et on doit trouver 2.
e) ![]()
f)construction….
g) h et i
seront corrigés en cours.
Pour
contacter le webmaster ![]() .
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.