DEVOIR SURVEILLE N°2
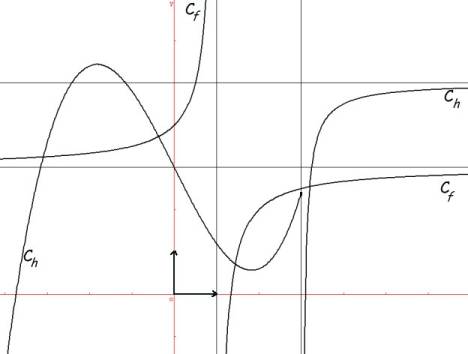
Exercice n°1 : 5 points
On considère les fonctions f et h définies par leurs courbes
respectives, dans le repère 
ci-contre.
1) Donner le domaine de définition de la fonction f.
2)
La fonction h est-elle
continue sur 
?
Expliquer.
3)
a) Donner la limite de f en 
.
b) Donner 
.
c) En déduire la limite de la composée de f suivie de h en 
.
4)
Donner la limite de la composée de h suivie de f en 
.
Exercice n°2 : 7 points
On considère la fonction g définie sur 
par 
.
1)
Calculer 
et démontrer que 
.
2) En déduire le tableau de variations (complet) de g.
3)
Démontrer que l’équation 
admet exactement trois solutions sur 
dont une entière.
Exercice n°3 : 9 points
Une entreprise fabrique un produit en quantité x,
exprimée en tonnes, avec 
.
Le coût marginal de fabrication exprimé en milliers d’euros est donné par la
fonction c définie par : 
pour 
. On appelle C la courbe représentative de la fonction c.
1)
Calculer 
. Donner une interprétation de ce nombre en terme
de coût.
2)
Trouver les nombres réels a, b et c tels
que 
pour tout 
.
3)
Calculer 
. En déduire les variations de c.
4) Pour quelle production, l’entreprise a-t-elle un coût marginal de production minimale ?
5)
Démontrer que C admet une asymptote oblique en 
d’équation 
.