Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

DEVOIR SURVEILLE N°5
Cliquez ici pour obtenir le document au format Word97 compressé avec winzip

Exercice n°1 : 5 points

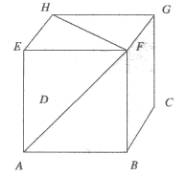On considère un cube ABCDEFGH, d’arête de longueur a (a réel strictement positif).

Soit I le point d’intersection de la droite (EC) et du plan (AFH).

1)      Calculer, en fonction de a, les produits scalaires suivants :  ,   et .

2)      En déduire que les vecteurs  et  sont orthogonaux.
On admettra de même que les vecteurs  et  sont orthogonaux.

3)      En déduire que le point I est le projeté orthogonal de E sur le plan (AFH).

4)      a) Justifier les résultats suivants : les droites (AF) et (EH) sont orthogonales, ainsi que les droites (AF) et (EI).
b) En déduire que la droite (AF)est orthogonale à la droite (HI).
c) Etablir de même que la droite (AH) est orthogonale à la droite (FI).

5)      Que représente le point I pour le triangle AFH ?.

Exercice n°2 :  15 points

Ce problème a pour objet d’étudier deux modèles d’évolution au cours du temps, d’une population de bactéries introduite dans un milieu de culture à l’instant t = 0.

Dans tout le problème, la population initiale sera de 1 Million d’individus, et on exprimera le temps t en heures.

Partie A : un premier modèle continu.

On notera  le nombre de bactéries à l'instant t (t = 0) ,  étant exprimé en millions d'individus .

On supposera que la fonction f est dérivable sur l'intervalle .

Dans les instants qui suivent l'ensemencement des bactéries, on considère que la vitesse d'accroissement des bactéries est proportionnelle au nombre de bactéries  en présence.

Ainsi il existe une constante a( a> 0) tel que .

1)      Résoudre cette équation différentielle (y' = a y) et en déduire l'expression de  en tenant compte de la population initiale: .

2)      En supposant que la population de bactéries double toutes les demi-heures, en déduire la valeur de a.

3)      On suppose désormais que la population de bactéries à l'instant test: .
a) Dans ce modèle, combien y a-t-il de bactéries au bout de 10 mn ? au bout de 1 h 40 ?
Quelle est la limite de f(t) en  ?
b) Au bout de combien de temps atteindra-t-on une population de 100 millions de bactéries ?

Tournez S.V.P

Partie B : modèle de Verbulst : équation logistique.

Le milieu étant limité ( en volume, en éléments nutritifs ...), le nombre de bactéries ne peut pas croître indéfiniment. Le modèle précédent ne peut donc pas s'appliquer sur une longue période.

En tenant compte de ces observations, Verhulst en 1838 a proposé le modèle suivant :

On appellera  le nombre de bactéries à l'instant t ( exprimé en millions de bactéries), la fonction g est une fonction strictement positive et dérivable sur l'intervalle  et est solution de l'équation différentielle :
(E) y' = y ln4 -k y² où k désigne une constante strictement positive dépendant des conditions expérimentales.

1)      Ajustement du modèle :
a) Montrer que la fonction g définie sur  par : vérifie (E) et la condition initiale: g(0) = 1.
b) Des mesures expérimentales montrent que la population finit par se stabiliser à 100 millions de bactéries. Trouver la valeur de k pour que la limite de g(t) en  soit 100.

2)      Comportement de ce modèle :
a) Montrer que pour tout ,0 < g(t) < 100.
b) Etudier le sens de variation de g et donner son tableau de variation complet sur .
c) Tracer, sur la feuille donnée en annexe (où figure y= f(t) du 2^ème modèle) la courbe représentative () de g.
d) Résoudre graphiquement puis par le calcul l'équation g(t) = 50. On notera t₀ cette solution.
e) Calculer  et étudier son signe. (On pourra pour cela dériver g' à partir de l'équation différentielle (E)). Etablir le tableau de variation de g' et en déduire que g' décroît à partir de t₀.
Comment interpréter cette propriété quant à l'évolution de la population de bactéries fournie par ce modèle?

3)       a. Montrer que, pour tout , .
b) En déduire une primitive G de g sur .